для функции копирования, не увеличивая

Задача 9.1. Постройте м.Т. для функции копирования, не увеличивая исходный алфавит ?.
Задача 9.2. Постройте программу м.Т., которая выполняла бы перенос непустого слова в заданное место ленты, т.е. для любого слова w (? \ {})* и n > 0 выполняла преобразование конфигураций:
Задача 9.3. Достройте программу м.Т. из леммы 9.1 на этапах 3 и 4.
Задача 9.4. Докажите, что односторонняя м.Т. построенная в лемме 9.2, корректно моделирует исходную м.Т.
Задача 9.5. Другой, по сравнению с конструкцией леммы 9.2, подход к моделированию двухсторонней ленты на односторонней заключается в том, чтобы содержимое правой полуленты хранить в четных ячейках а содержимое левой полуленты - в нечетных, поместив в 1-ю ячейку специальный маркер. Постройте программу, реализующую этот подход (ее достоинство - увеличение алфавита ленты всего на 1 символ).
Задача 9.6. Достройте программу м.Т. из леммы 9.4 на этапах 1, 3 и 5.
Задача 9.7. Построить программы машин Тьюринга, вычисляющих следующие функции.

• Перевод из двоичной системы в унарную: fbu(n(2))= |n.
• Сложение и вычитание в двоичной системе: sum(n*m)=n+m и
  
  совпадает с - при n
  
  m и
  
  при m > n).
• Умножение в двоичной системе: mul(n*m)= n ? m. ( Реализуйте алгоритм умножения "в столбик".)
• Возведение в степень: exp(n*m)= nm.
• Извлечение квадратного корня:
  
  .
• Логарифмирование: log(n)=
  
  log2n
  
  .
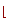• Деление:
  
• Остаток от деления: rest(n*m) = n mod m.
• Функция выбора аргумента:
  
  .

Задача 9.8. Используя машины Тьюринга из предыдущей задачи, построить программы машин Тьюринга, вычисляющих следующие функции.

1. 
   
   
   
   
2. 
   
   
   
   
3. 
   
   
   
   
4. 
   
   
   
   

Задача 9.9. Докажите, что всякую арифметическую функцию f(x), вычислимую на некоторой м. Т. M = <Q, ?, P,q0, qf>, можно также вычислить на м. Т. M',, алфавит ленты которой содержит лишь два символа и |. (Указание: используйте для моделирования одного символа из ? блок из нескольких подряд идущих ячеек, содержащих его код в алфавите {, , | }) и замените каждую команду M группой команд, обрабатывающих соответствующий блок ячеек).


Задача 9.10.
Построить машину Тьюринга, определяющую по слову x в алфавите {1, 2} симметрично ли оно, т. е. вычисляющую функцию:

Задача 9.11.
Построить машину Тьюринга, сравнивающую два слова x=x1x2… xn и y=y1y2… ym в алфавите {1, 2, 3} лексикографически: или для некоторого непустого слова x' выполнено y = x x'. Эта машина Тьюринга должна вычислять функцию:


Содержание раздела

---