Сокращенные УБДР
Когда порядок переменных зафиксирован, то достаточно просто можно по произвольной УБДР для функции построить минимальную УБДР, реализующую данную функцию.
Определение 3.3. УБДР называется сокращенной, если
- из любой внутренней вершины v ее 0-сын и 1-сын не совпадают;
- нет такой пары внутренних вершин u и v, для которых поддиаграммы с корнями u и v являются изоморфными (т.е. взаимно однозначно отображаются друг на друга с сохранением всех меток).
Смысл этого определения понятен: если из некоторой вершины v оба ребра ведут в одну вершину, то такая вершина v не нужна, а если имеются две вершины с одинаковыми поддиаграммами, то их можно слить. Определим два типа эквивалентных преобразований УБДР.
Правило сокращения: если 0-сын и 1-сын вершины v совпадают и равны w, то удалить v, перенаправив все входящие в нее ребра в вершину w.
Правило слияния: если вершины v и w помечены одной переменной и имеют одинаковых 0-сыновей и 1-сыновей, то удалить вершину v, перенаправив все входящие в нее ребра в вершину w.
На следующем рисунке показаны преобразования по этим правилам.
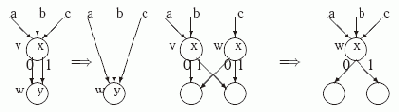
Рис. 3.4. Правило сокращения Правило слияния
Следующая простая теорема показывает, что применимость этих двух правил является критерием несокращаемости УБДР.
Теорема 3.1.
УБДР D является сокращенной тогда и только тогда, когда к ней не применимо ни правило слияния, ни правило сокращения.
Доказательство.

? Пусть к УБДР D нельзя применить правило сокращения. Тогда в ней нет вершин с совпадающими 0- и 1-сыновьями и выполнено условие (1). Пусть к УБДР D нельзя применить правило слияния. Тогда из следующей леммы можно заключить, что в D нет пары вершин, поддиаграммы которых являются изоморфными, и следовательно, выполнено условие (2).
Лемма 3.2. Если в D есть такая пара вершин u и v, для которых поддиаграммы с корнями v и w являются изоморфными, то в D имеется и пара вершин v', w' с попарно одинаковыми 0- и 1-сыновьями и, следовательно, к D применимо правило слияния.
Доказательство леммы проведем индукцией по высоте h поддиаграмм Dv и Dw с корнями v и w, соответственно (так как Dv и Dw изоморфны, то их высоты, т.е. длины максимальных путей из корней до стоков, одинаковы).
Базис: h=1. В этом случае 0- и 1-сыновьями вершин v и w являются одинаковые стоки.
Шаг индукции. Предположим, что утверждение верно для h=k. Пусть Dv и Dw - поддиаграммы высоты h=k+1. Пусть v0 и w0 - это 0-сыновья вершин v и w, соответственно, а v1 и w1 - их 1-сыновья. Если v0=w0 и v1=w1, то в качестве v', w' подходят сами v и w. Если же для некоторого i




Из теоремы 3.1 непосредственно следует, что, применяя к произвольной УБДР правила сокращения и слияния, мы, в конце концов, получим сокращенную УБДР. Чтобы эта процедура работала эффективо, нужно применять правила в порядке "снизу-вверх". Мы опишем этот алгоритм для "естественного" порядка переменных: x1, … , xn.
Алгоритм СОКРАЩЕНИЕ-УБДР
Вход: УБДР D для функции f(x1, … , xn).
Выход: сокращенная УБДР для

1. Занумеруем множество вершин D: V = {v1, v2, …, vm}; 2. ДЛЯ i = n, n-1, …, 1 ВЫПОЛНЯТЬ 3. { 4. V(i) = { v | v помечена переменной xi }; /* Применение правила сокращения: 5. ДЛЯ КАЖДОЙ v

Пример 3.1. Рассмотрим пример применения алгоритма СОКРАЩЕНИЕ-УБДР, показанный на следующем рисунке.
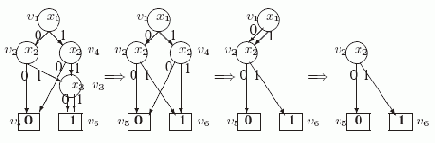
Рис. 3.5. Применение алгоритма СОКРАЩЕНИЕ-УБДР
На исходной УБДР слева все вершины уже занумерованы. Стрелки разделяют УБДР, получаемые после очередных итераций основного цикла в строках 2 - 19. При первом исполнении цикла i=3, V(3) = {v3}. Для вершины v3 условие в строке 6 выполнено (w= v6), поэтому применяется правило сокращения и эта вершина удаляется, а ее входы направляются в v6. При следующем исполнении цикла i=2, V(2) = {v2, v4}. После цикла в строках 5 - 10 key(v2)= {5, 6} и key(v4)= {5, 6}. После сортировки u1=v2, u2 = v4. В цикле в строках 13-18 для u2 выполнено условие в строке 14. Поэтому применяется правило слияния и вершина v4 удаляется, а ее вход передаeтся вершине v2. При третьем исполнении цикла i=1, V(1) = {v1}. Для вершины v1 условие в строке 6 выполнено (w= v2), поэтому применяется правило сокращения и эта вершина удаляется.
Оказывается, что построенная алгоритмом УБДР является единственной и минимальной для заданного порядка.
Теорема 3.2.
- Алгоритм СОКРАЩЕНИЕ-УБДР строит сокращенную УБДР, эквивалентную исходной УБДР D.
- Эта сокращенная УБДР является при данном порядке переменных единственной (с точностью до изоморфизма) и минимальной.
Доказательство первого пункта непосредственно следует из выполнения критерия теоремы 3.1, так как к результирующей диаграмме никакое правило сокращения или слияния неприменимо.
Доказательство второго пункта основано на следующем индуктивном утверждении:
Лемма 3.1.
После выполнения i-ой итерации алгоритма в полученной диаграмме для каждой подфункции f(?1, ?2, …, ?_{i-1},xi, …, xn) (?k

Напомним, что функция f(x1, x2, …, xi, …, xn) существенно зависит от переменной xi, если существуют такие два набора значений аргументов (?1, …, ?i-1, 0, ?i+1,…, ?n) и (?1, …, ?i-1, 1, ?i+1,…, ?n), различающиеся только значением xi, на которых f принимает разные значения: f(?1, …, ?i-1, 0,?i+1, …, ?n)

Доказательство этой леммы и вывод из нее утверждения 2 теоремы 3.2 оставляем в качестве задач 3.2 и 3.3.
