Основные определения

Одним из предшественников УБДР являются бинарные деревья решений.

Определение 3.1.

Бинарное дерево решений (БДР) - это бинарное дерево T=(V,E), все внутренние вершины которого помечены переменными, а листья - значениями 0 или 1. Из каждой внутренней вершины v выходят 2 ребра, одно помечено 0, другое - 1; вершина w0, в которую ведет ребро, помеченное 0, называется 0-сыном v, а вершина w1, в которую ведет ребро, помеченное 1, называется 1-сыном v.

Такое дерево, вершины которого помечены переменными x1, …, xn реализует булеву функцию f(x1, …, xn), если для каждого набора значений переменных ?1, ?2, …, ?n ветвь в дереве, соответствующая этому набору (из вершины xi идем по ребру, помеченному ?i), завершается листом с меткой f(?1, ?2, …, ?n).

Пример 3.1. Например, рассмотрим изображенное ниже БДР T1 (на всех рисунках предполагается, что ребра направлены сверху вниз).

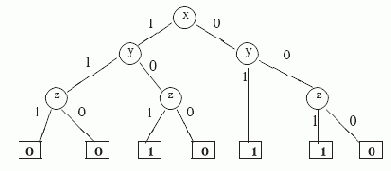
Рис. 3.1.

По определению T1 реализует функцию f1(x,y,z), представленную в таблице 3.1.

Таблица 3.1. Функция f1(x, y,z), реализуемая БДР T1 на рис.3.1

xyzf(x,y,z)

0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	0
1	1.	1	0

Нетрудно построить ДНФ этой функции: f(x, y, z) = (¬ x

(¬ y

z).

УБДР являются модификацией БДР, в которой все листья с одной меткой представлены одной вершиной, в каждую вершину может входить несколько ребер, возможен выбор порядка появления переменных на ветвях.

Определение 3.2. Пусть зафиксирован некоторый порядок n переменных

: x

(1), …, x

(n).

Упорядоченная бинарная диаграмма решений относительно порядка переменных

- это ориентированный граф без циклов с одним корнем, в котором

существует лишь две вершины, из которых не выходят ребра; они помечены константами 0 и 1 и называются стоками;
остальные (внутренние) вершины помечены переменными и из каждой из них выходят два ребра, одно помечено 0, другое - 1;
порядок, в котором переменные встречаются на любом пути из корня в сток, совместим с
, т.е. если из вершины, помеченной x
(i), есть путь в вершину, помеченную x
(j), то i < j.

Как и в случае БДР, УБДР реализует булеву функцию f(x1, …, xn), если для каждого набора значений переменных ?1, ?2, …, ?n путь в диаграмме, начинающийся в корне и соответствующий этому набору (из вершины xi идем по ребру, помеченному ?i), завершается стоком с меткой f(?1, ?2, …, ?n).

Из этого определения непосредственно следует, что каждая внутренняя вершина диаграммы v, помеченная переменной x

(k), является корнем поддиаграммы, которая включает все вершины диаграммы, достижимые из v, и реализует некоторую функцию fv( x

(k),x

(k+1), …, x

(n)) от (n -k +1) переменных x

(k),x

(k+1), …, x

(n). При этом ее 0-сын w0 является корнем поддиаграммы, реализующей функцию fw0(x

(k+1), …, x

(n)) =fv( 0, x

(k+1), …, x

(n)), а 1-сын w1 - корень поддиаграммы, реализующей функцию fw1(x

(k+1), …, x

(n)) =fv( 1, x

(k+1), …, x

(n)). Пусть диаграмма реализует функцию f(x1, … , xn) = f'(x

(1), …, x

(n)) и ?

(1),… , ?

(k-1) - это набор значений переменных x

(1), …, x

(k-1), который соответствует пути из корня в вершину v (таких наборов может быть несколько). Тогда fv( x

(k), …, x

(n))= f'(?

(1),… , ?

(k-1),x

(k), …, x

(n)).

Пример 3.2. Реализуем с помощью УБДР функцию f1(x,y,z), представленную выше в примере 3.1, с помощью БДР T1 и таблицы 3.1.

Вначале зафиксируем порядок переменных: x < y < z. Объединив листья с одинаковыми метками и две z- вершины с одинаковыми потомками, получим УБДР D1, приведенную на рис.3.2.

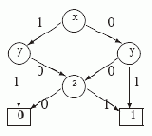
Рис. 3.2.

Ясно, что реализация функции f1(x,y,z) с помощью УБДР D1 намного компактнее, чем с помощью БДР T1.

Под сложностью L(D) УБДР D будем понимать число внутренних вершин в D. Например, L(D1)=4. Может ли сложность диаграммы для некоторой функции зависеть от порядка переменных? Да! Рассмотрим порядок переменных y < x < z. Как показывает следующий рисунок, относительно этого порядка функцию f(x,y,z) можно реализовать УБДР D2 со сложностью L(D2)=3.

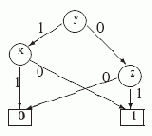
Рис. 3.3.

Содержание раздела

Главная сайта